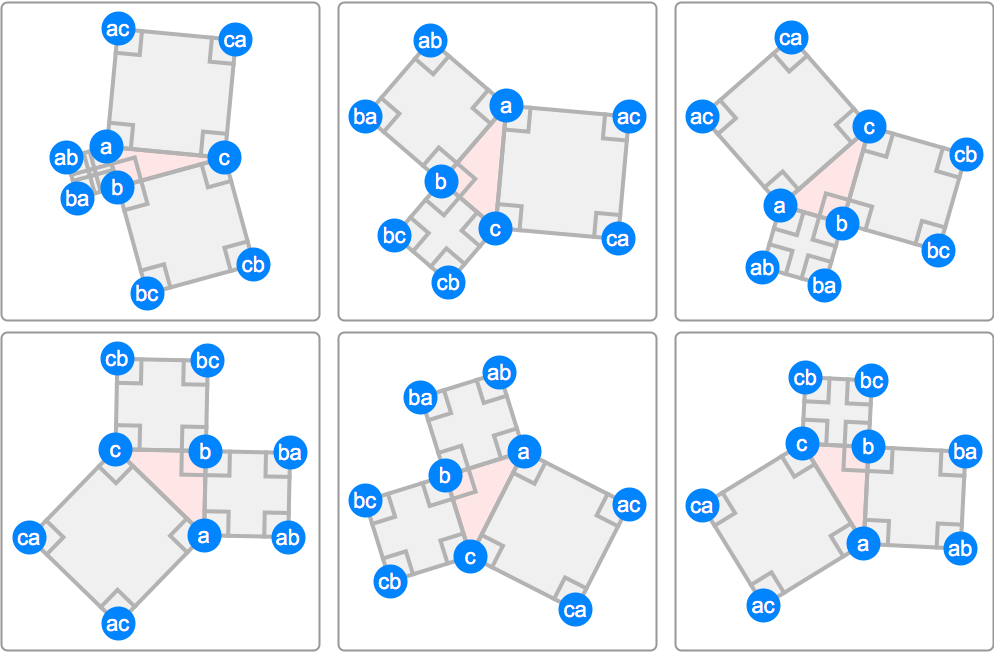
」 定理はたくさんありますよ。 ①面積=たて×よこ ②向かい合う辺は平行 ③向かい合う辺の長さは等しい ④対角線の長さは等しい ・・・などなど。内容 定理 共円四角形を対角線によって重なりのある四つの三角形に分割する(二つある対角線ひとつごとに二つの三角形に分割する)とき、それら四つの三角形の内接円の中心は一つの長方形の各頂点になっている。 より具体的に、 abcd を勝手な共円四角形とし、 m 1, m 2, m 3, m 4 をそれぞれ abd方べきの定理 方方方方べきのべきの定理 方べきの定理は教科書で次のように紹介され、3つの図形が示されています。 点Pを通る2直線が、与えられた円と点A,Bおよび点C,Dで交わるとき,次の式が成り
対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス
長方形 の 定理
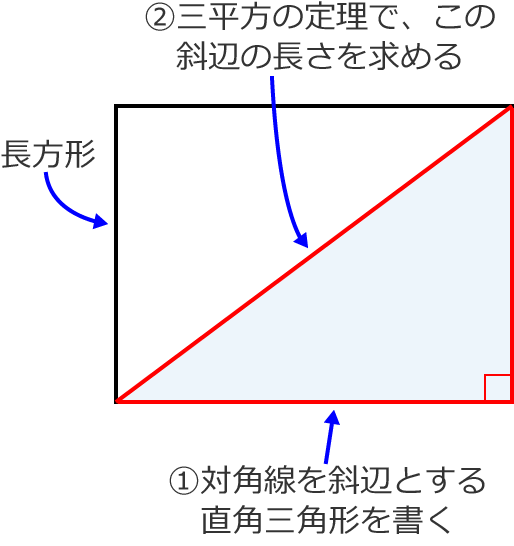
長方形 の 定理- 長方形の対角線の求め方の公式はなんでつかえるの?? だがしかし、 なぜ公式で対角線の長さが計算できちゃうんだろう??? って疑問に思うよね。 その理由はずばり、 直角三角形で三平方の定理をつかっているから なんだ。 長方形で対角線をひいたら、長方形は円に内接するから、長方形にトレミーの定理を適用すれば三平方の定理(ピタゴラスの定理)が現れてくる。 トレミー( プトレマイオス )は150年ころアテネやアレクサンドリアで活躍した学者で古代天文学の中心人物であった。
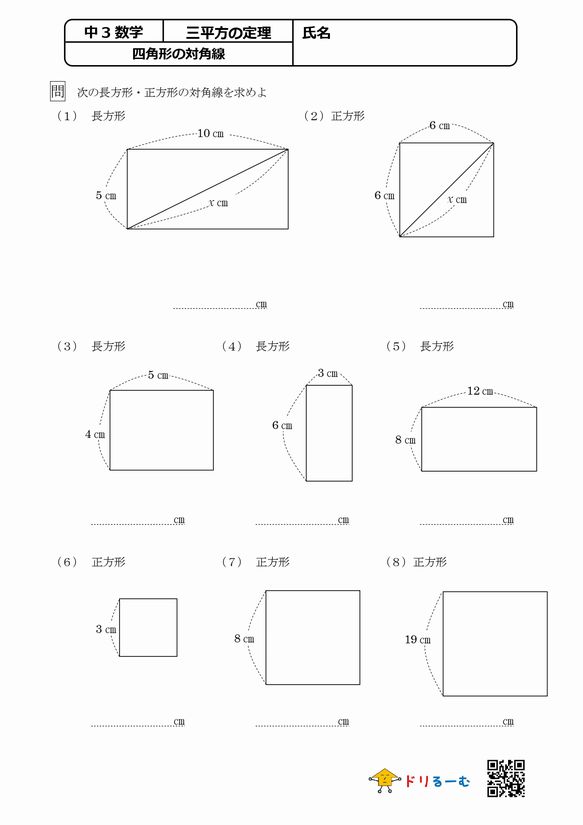



三平方の定理 四角形の対角線 ドリるーむ
1.長方形の対角線の長さは等しい。(証明) 2.ひし形の対角線は垂直に交わる。(証明) 3.正方形の対角線の長さは等しく、垂直に交わる。 図形を選び、頂点をドラッグして、対角線がどういう条件のとき長方形やひし形になるか調べよう。定理一覧 円を含む図形 方べきの定理 トレミーの定理 シムソンの定理 シュタイナーの定理 アルハゼンの定理 ニュートンの定理 九点円の定理 フォイエルバッハの定理 ターレスの定理 パスカルの定理 アポロニウスの定理 ブリアンショの定理長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する
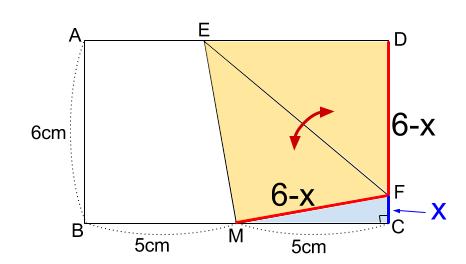
ABFで三平方の定理を使うと (10−x) 2 =6 2 x 2 100−xx 2 = 36x 2 −x=36−100 x=64 x= 16 5 答 16 5 cm ※ 3辺のうち1辺だけ長さがわかって、残りのうち1辺がx, もう1辺がxを用いた式にする問題は多い。 練習 ≫長方形(ちょうほうけい)、矩形(くけい)(英 rectangle )は、4つの角がすべて等しい四角形である。 平行四辺形の一種であり、平行四辺形の性質をすべて満たすほか、次の性質を有する。 4つの内角はすべて直角に等しい。;長方形 対角線の長さが等しく、それぞれの中点で交わるとき長方形になる。 証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行四辺形abcdの性質より ab=dc 1 bc=cb(共通) 2
平行軸の定理(復習) 重心 a m 重心を通る軸のまわ りの慣性モーメント i g それに平行な軸のま わりの慣性モーメント i i i ma 2 = g 工学院大学の学生のみ利用可:印刷不可:再配布不可(c)加藤 三平方の定理(ピタゴラスの定理)を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、 13² = 5² x² x = 12 あら不思議! 長さがわからない直角三角形の辺を求めることができたね。 >> 三平方の定理線積分とGreen の定理 f(x;y) を平面内の領域D 上の連続関数とする。またC をD に含まれる連続曲線 (例) 長方形R =




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
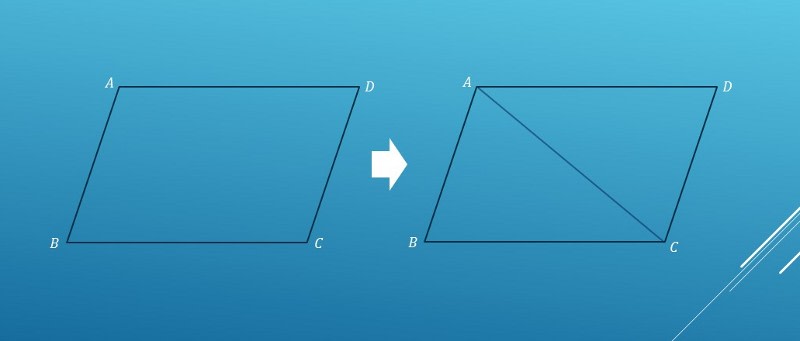



高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座
は合同な長方形※である。 となり合う面は、それぞれ垂直である。 1つの辺は4つの辺と垂直で3つの辺と 平行である。 立方体 6つの正方形で囲まれた箱の形 直方体を参照。 すべての面が合同。 角柱 2つの合同な多角形と長方形※で囲まれ側面が長方形※6三平方の定理 ガイダンス 式と陰陽師 式を操る 式を立てる 長方形の面積を求める 正方形の面積と一辺の長さとの関係 電卓のしくみ ×= と√の働きを探る アラビアの数学 アラビアンナイトとアラビア数字 アル=クワリズミと二次方程式公式(三平方の定理) 対角線=√(底辺 2 +高さ 2 ) 電卓で計算する方法 例:2×1cmの長方形の場合 2→×→=→M→ 1→×→=→M 3 内容の取扱い (2) 内容の「B図形」の(2)のイに関連して,正方形,ひし形,長方形を取り扱う際には,これらが平行四辺形の




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス
4つの角の大きさが全て等しい四角形を長方形という。 定理 長方形の2組の向かい合う辺はそれぞれ平行で長さが等しい。 定理 長方形の対角線はそれぞれ中点で交わる。中線定理の証明の方針 教科書にも載っている中線定理ですが,正弦定理や余弦定理などの花型公式と比べるとやや地味な感じがします。 しかし,中線定理は様々な手法で証明できるので, 図形の証明問題のよい題材です。 このページでは中線定理の証明長方形pacdを1周した時の2次元のグリーンの定理の形になっている。 ここで、以下の事に気づく人は多いと思う。 3次元の経路を考える場合、いかなる経路を通っても同じという事を言うには 3つの2次元のグリーンの定理を満たす必要があるのでは?




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7819 Pdf
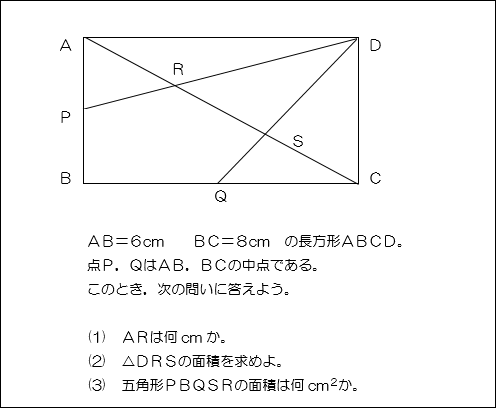
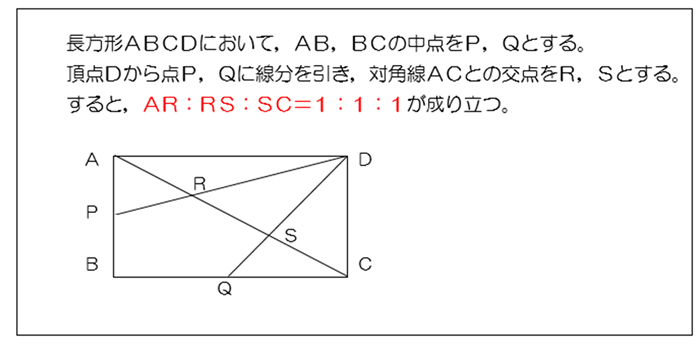
微分積分続論レポート(h) id 氏名 * 解答に際し,講義で紹介した定理,命題など,さらにレポート問題の結果は証明なしに用いて良い. * レポートにはa4版用紙を用いよ. * 提出は次回講義時. 問題 グリーンの定理を用いて,以下の線積分の値を求めよ. (1) (0∫;0);(2;0);(2;2)(0;2)を頂点と対角線3等分の定理より AR= cm 2 対角線3等分の定理より 2 (3) 五角形PBQSR=長方形- APD- DQC- DRS =48-12-12-8=16cm 2 ※この定理を知らなければ・・・・ちょっと大変かも。(@_@) その2 (考え方) 対角線3等分の定理 をイメージしてみよう。13 応用3 整数長の辺を持つ長方形への分割 次の定理を奇点定理を使って証明しよう. 定理5 長方形abcd の内部を,小長方形へ分割する.(図3 参照) このとき,すべての 小長方形で縦か横の長さが整数ならば,もとの長方形abcd でも縦か横の長さが整数と なる.




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



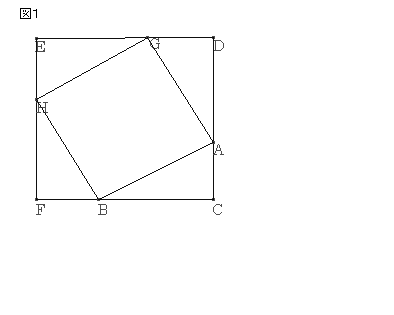
四角形の4つの辺の中点を結んでできる四角形
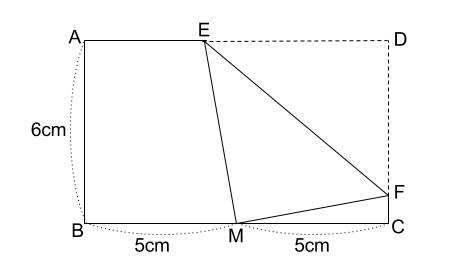
この長方形を、下の図のように、 \(d\) が \(bc\) の中点 \(m\) と重なるように折ります。 このとき、 \(CF\) の長さを求めなさい 解説初見ではなかなか戸惑う問題でしょうか。そのため長方形の縦と横の長さから三平方の定理を使って対角線の長さを出すことができる。 例縦2cm, 横3cmの長方形の対角線を求める。 2cm 3cm x 対角線を引いて直角三角形をつくる。 三平方の定理にあてはめる。 x 2 =2 2 3 2 x 2 =49 x 2 =13に分けて寄せ集めて1つの長方形 から1つの正方形を作る a ‚ b, a • 4b x (a¡ p ab) = p ab a より x = p ab¡b x • b , a • 4b a b p ab x ピタゴラスの定理を用いて, 下図のように p ab の長さの辺を作図 し, 上図のようにして長方形から面積の等しい正方形を作る a¡b ab




3分でわかる 長方形の定義 Qikeru 学びを楽しくわかりやすく




中点連結定理を利用した証明 チーム エン
はラテン長方形である m =n であるようなラテン長方形をラテン方陣と呼ぶが,ラテン長方形からラテン方陣への拡大可能性 は次の定理で与えられる 定理271 M はm黄金長方形の作図は意外に簡単。コンパスと定規を使って描いてみましょう。 正方形abcdを描き,辺bcの中点をeとする。 点eを中心としてedを半径とする円弧を描き,bcの延長との交点をgとする。即ちed=eg。 長方形abghを描けば,黄金長方形の出来上がりです。 目次 きりぬき 新しい『小学校学習指導要領解説算数編』より リンク集 トピック1 正方形と長方形の紙を折って,箱を作るには トピック2 排反的な(exclusive)定義と包摂的な(inclusive)定義 トピック3 オーダーとの関わり きりぬき 第2学年で,長方形や正方形を学習する時点では,それら



ピタゴラスの定理 ウソの国ー詩と宗教 戸田聡 St5402jp
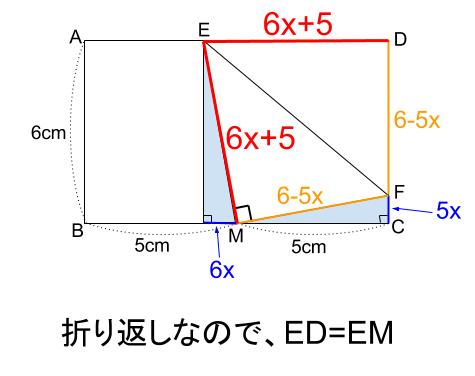



折り返しと三平方の定理 中学数学の無料オンライン学習サイトchu Su
方べきの定理とその統一的な証明 方べきの定理とは,円と点 P P P と2本の直線が作る図形において, P A 1 × P A 2 = P B 1 × P B 2 PA_1\times PA_2=PB_1\times PB_2 P A 1 × P A 2 = P B 1 × P B 2 が成立するという定理です。方べきの定理は全部で3パターンあります。リーンの定理は成り立たない Cを単位円に反時計回りに向き付けしたものとする I= ∫ C y x2 y2 dx x x2 y2 dy を求める。 @ @y (y x2 y2) = @ @x (x x2 y2) = x2 y2 (x2 y2)2 なので、形式的にグリーンの定理を用いるとI= 0 しかし、被積分函数は原点で連続ではない。ピックの定理の証明 すぐるの算数カルチャー講座 ピックの定理 面積 = まわりの点の数 ÷ 2 + 内部の点の数 - 1 ピックの定理を,以下の順で証明していきます。 1.長方形において,ピックの定理は成り立つ。 2.直角三角形において,ピックの定理
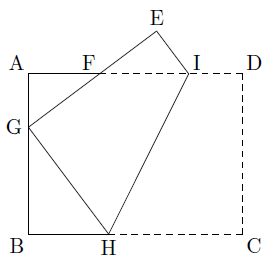



図形の折り返し まなびの学園
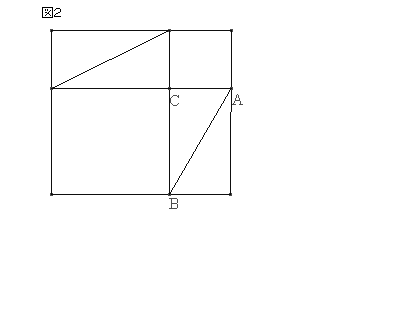



ピタゴラスの定理 の別証明集
この定理はとても簡単で、図形的な意味も自然です。 でも、長方形になるところがくずれ過ぎです。あくまで正方形になるようにするにはどうしたらいいのでしょうか。 余弦定理は二つあって式が対称であることに注目します。 中線定理三平方の定理(発展) 折り返し 次の問いに答えよ。 長方形abcdの頂点cを辺ad上に折り返した。 そのときの折り目efの長さを第3回目講義:ストークスの定理(線積分⇔面積分) (12月11日) (12月18日) (1月15日) 講義内容:ベクトル場における積分定理 第1回目講義:平面におけるグリーンの定理 (テキストp144p149) GGreen () グリーンの定理に関する原著論文
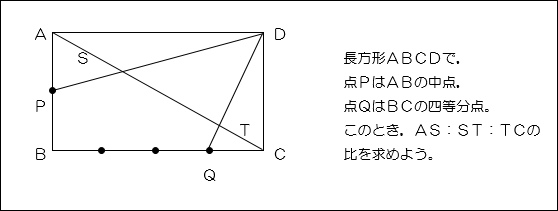



授業実践記録 数学 新しい 定理 とその活用 啓林館



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配
長方形の代わりに台形で近似すると,収束がもっと早くなります。 ここまでの説明は, \(0 \leqq x \leqq 1\) の区間を \(n\) 等分して小区間の右端で長方形の高さを決めましたが,左端を長方形の高さとしても結果は変わらないことを付け加えておきます。 長方形とは、4つの角がすべて直角の四辺形のことを指します。 AutoCADで長方形を作成するには、一般的には長方形コマンド又は線分コマンドを使用します。 この2つの違いを説明します。 目次へ戻る 1-1.長方形コマンドと線分コマンドで作成する違いは?図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し
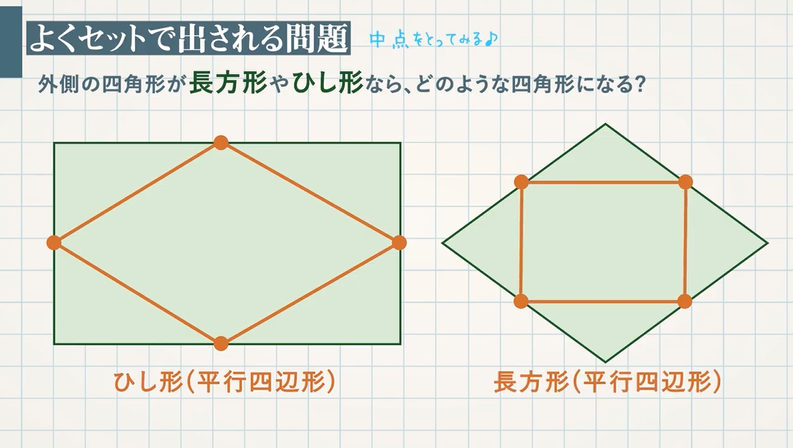



中点連結定理を使った平行四辺形であることの証明 教遊者



三平方の定理で体積と表面積を求める問題なのですが 底面が正方 Yahoo 知恵袋
定理より、長方形の面積は \(F(adx)F(a)\) であり、これは \(f(a)\cdot dx\) と等しくなります。そして微分は、この面積を \(dx\) で割ったものなので、\(f(a)\) と等しくなります。
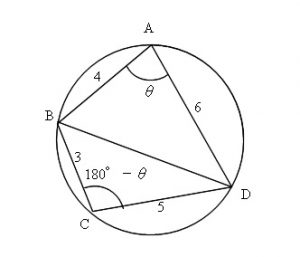



円に内接する四角形の面積の求め方と定理の使い方
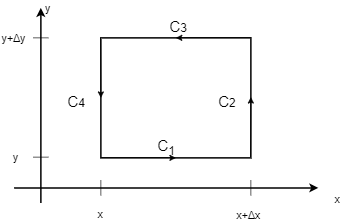



大学物理のフットノート 物理数学 ストークスの定理
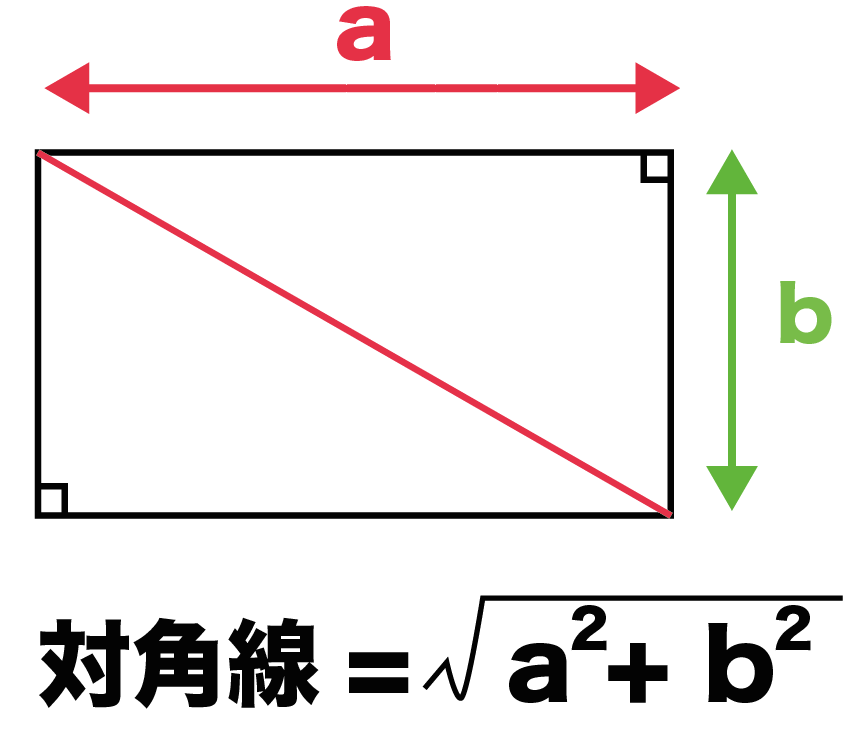



3秒で計算 長方形の対角線の求め方がわかる公式 Qikeru 学びを楽しくわかりやすく




山と数学 そして英語 方べきの定理
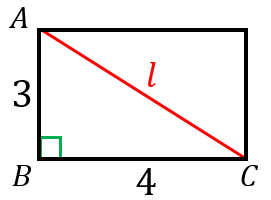



長方形の対角線の長さの求め方 具体例で学ぶ数学



3
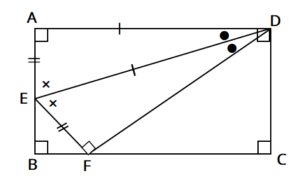



高校入試対策数学 折り返し図形と三平方の定理の問題 中学生勉強サイトあかね先生




中学校数学 証明のコツ 年01月



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学
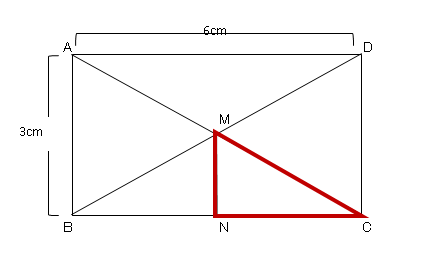



三平方の定理の応用 1 ネット塾
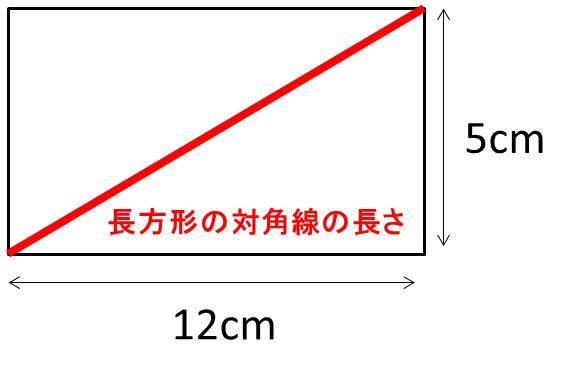



Excel エクセルで対角線の長さを計算する方法 長方形



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形



画像をダウンロード 平行 の 定義 あなたのためのぬりえ
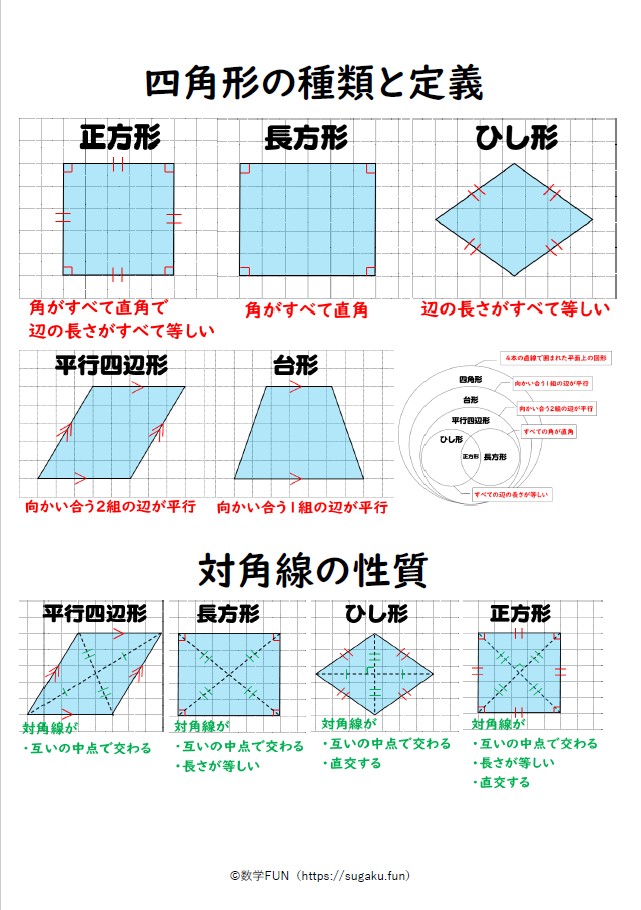



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




この2問が分かりません 高校の数学課題です 三平方の定理を使うのは分かるのですが Clear
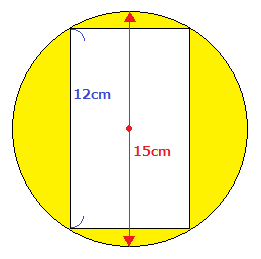



円の中の長方形の問題の解答と解説 多目的ルーム 楽天ブログ



3 14 ストークスの定理



授業実践記録 数学 新しい 定理 とその活用 啓林館
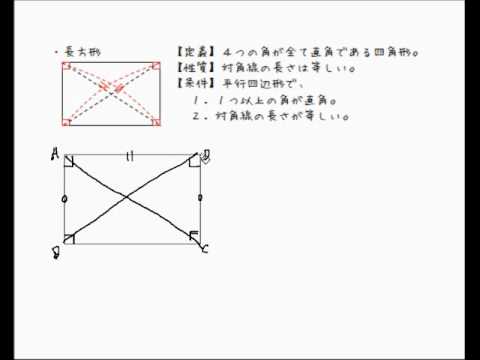



長方形の定義 性質 条件 Youtube



Http Www Edu City Misato Lg Jp Secure 0526teigi Teiri Kotae Pdf



3




3秒で計算 長方形の対角線の求め方がわかる公式 Qikeru 学びを楽しくわかりやすく



三平方の定理と平面図形の問題です 下の図は 長方形abcdを Bfを折り Yahoo 知恵袋




1つの定理を証明する99の方法 フィリップ オーディング 冨永 星 本 通販 Amazon




三平方の定理 四角形の対角線 ドリるーむ
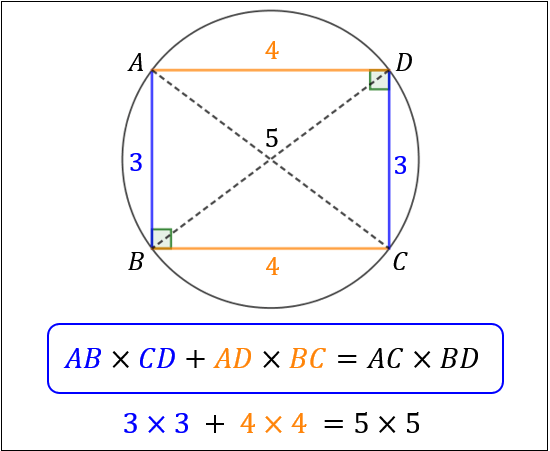



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




世界一わかりやすい数学問題集中3 7章 三平方の定理




長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく



折り返しと三平方の定理 中学数学の無料オンライン学習サイトchu Su




無料 中3数学 発展 応用問題 解答プリント 329 図形の相似4 中点連結定理




高校数学 Sin A B 加法定理を図 長方形 で表すと 江南の塾 ネクサス 勉強のやり方専門塾 小中高一貫の少人数個別指導塾




ある長方形の問題の8通りの解答 数学徘徊記
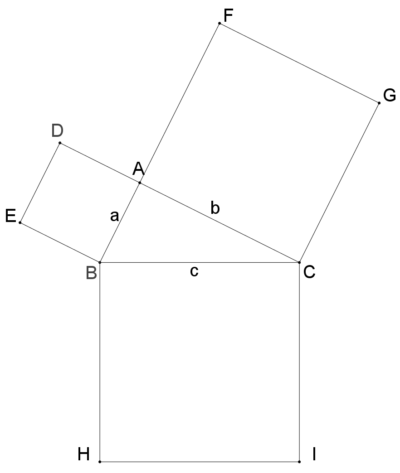



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも




三平方の定理の利用 2 きっずゼミ子育て応援ブログ



折り返しと三平方の定理 中学数学の無料オンライン学習サイトchu Su
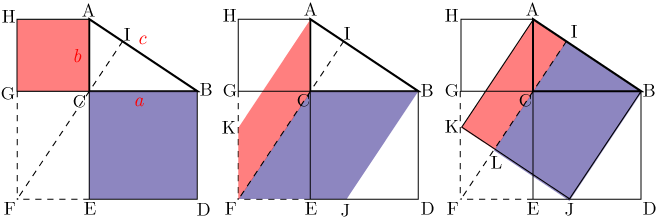



三平方の定理 ピタゴラスの定理




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
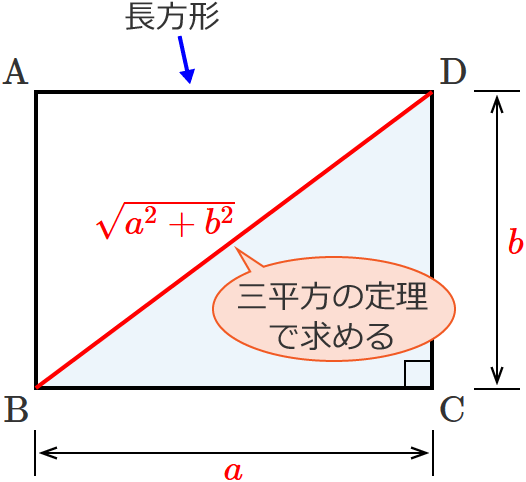



長方形の対角線の長さの求め方




中3 中点連結定理の証明です やり方も教えてください Clear



長方形を正方形に




三平方の定理 画像のように縦が4センチ横が8センチの長方形abcdの紙を 数学 教えて Goo
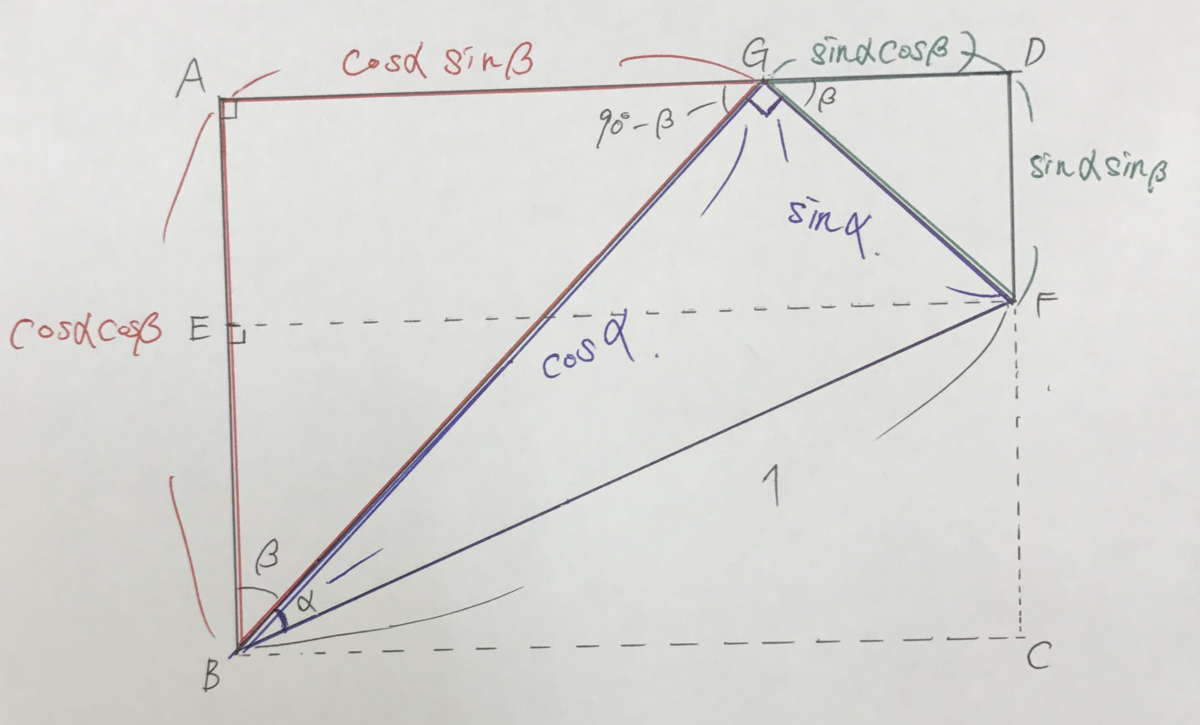



15 加法定理 その2 遊んで加法定理を理解しよう 医学生gの数学ノート




長方形の対辺は等しい っていう定理ありますか Clear




中学校数学 証明のコツ 年01月
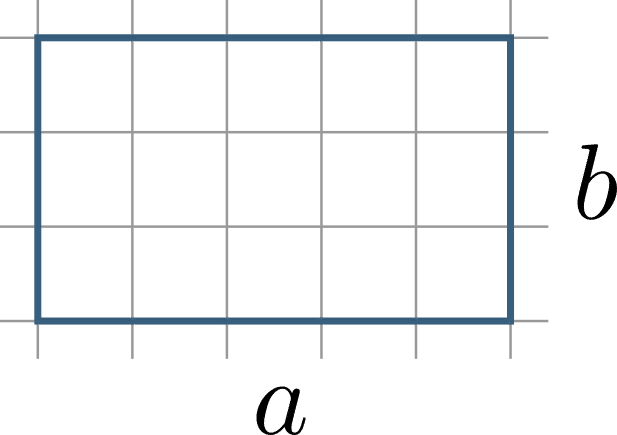



ピックの定理の証明 特殊な長方形 マスマチコ Note



三平方の定理




数学にとって証明とはなにか ピタゴラスの定理からイプシロン デルタ論法まで ブルーバックス 瀬山 士郎 本 通販 Amazon
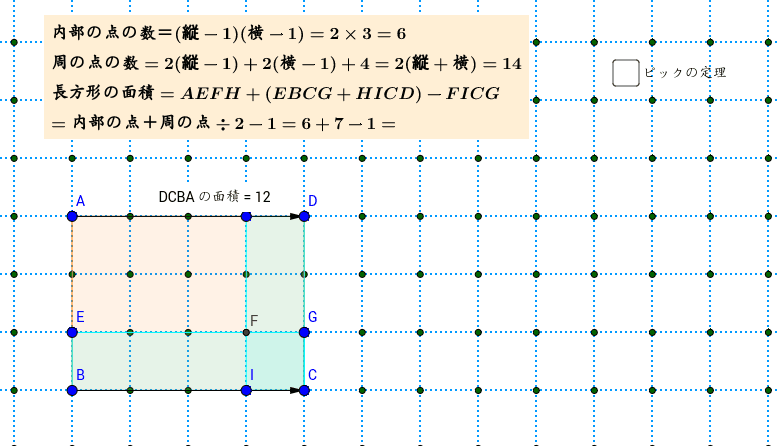



長方形におけるピックの定理 Geogebra



ピタゴラスの定理 の別証明集
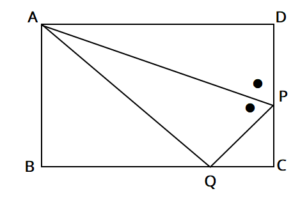



高校入試対策数学 折り返し図形と三平方の定理の問題 中学生勉強サイトあかね先生




三平方の定理の利用 立体 チーム エン



三平方の定理




発展講座 トレミーの定理の使い方と証明 南数英指導会 南ノートブログ版



長方形を正方形に



1




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



1



長方形の対角線の長さの求め方



授業実践記録 数学 新しい 定理 とその活用 啓林館



Www Tsumugi Ne Jp Member St2 54 Pdf



ピタゴラス Pythagorean の定理 Wolfram言語 12の新機能




加法定理の長方形からの確認 Den Of Hardworking



四角形efghがひし形や長方形になるときはどんなときか というレ Yahoo 知恵袋



四角形の4つの辺の中点を結んでできる四角形



高校入試 英語 数学 学習 三角形と四角形 特別な平行四辺形




中学校数学 証明のコツ 年01月
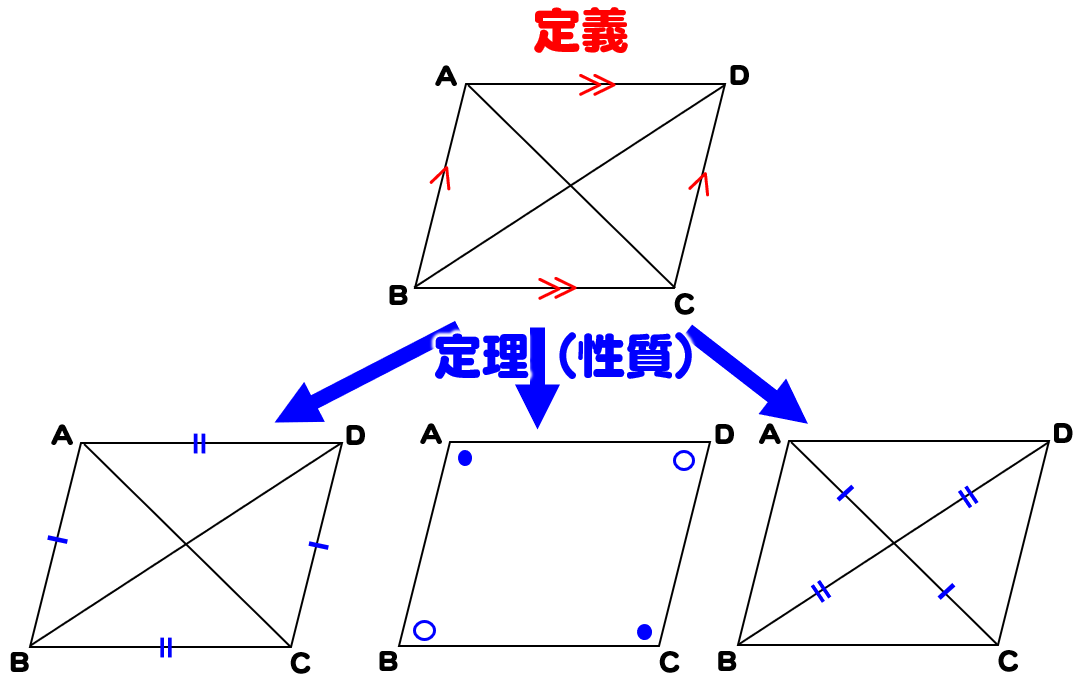



平行四辺形の定義と性質 証明問題の解き方 数学fun
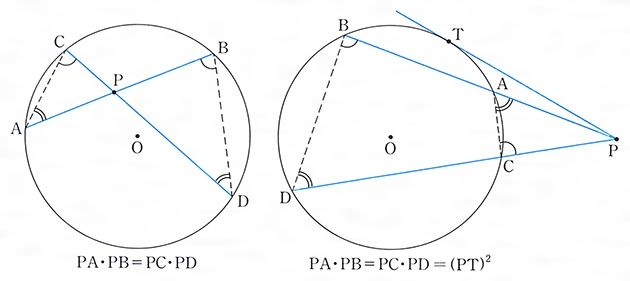



方べきの定理とは コトバンク



リンクの図に示すように 長方形の中に直角三角形が2つあります ある程度わかっている寸法をもとに短辺abの長さを求めると どういう値になりますか Quora
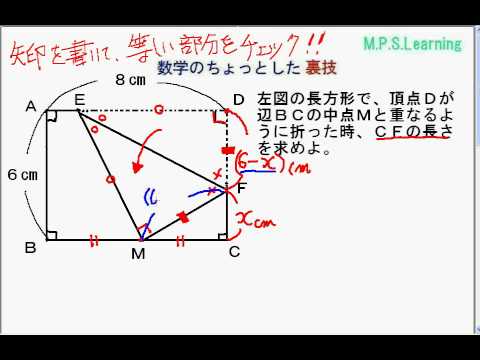



中3数学 三平方の定理の応用 折り曲げ 2 Youtube




スタディピア 図形




Abcd Pqrs Abcd Pqrs Abcd Descubre Como Resolverlo En Qanda
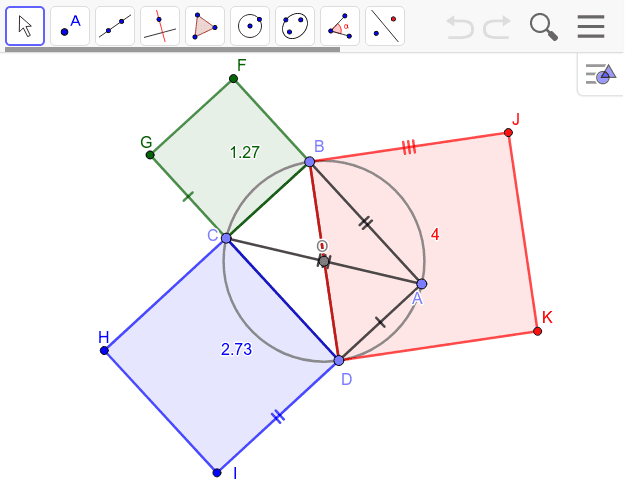



プトレミーの定理 Geogebra



問題159 正方形の問題




中点連結定理を使った平行四辺形であることの証明 教遊者
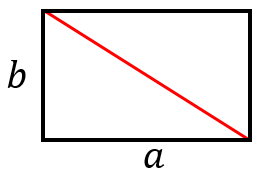



長方形の対角線の長さの求め方 具体例で学ぶ数学




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典



Tossランド 特別な平行四辺形




余弦定理の発見 Geogebra
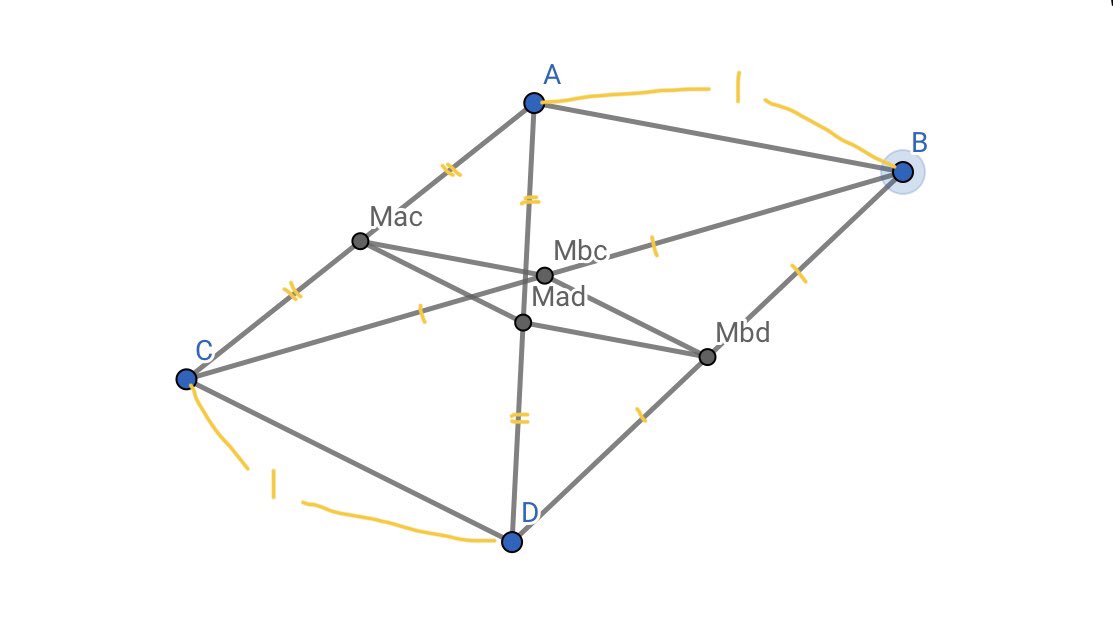



O Xrhsths Show Sto Twitter 中点連結定理から求める四角形の各辺の長さは1 2で等しい 従って求める四角形はひし形 また対称性よりmacmbd Madmbc 従って求める四角形は長方形 よってひし形かつ長方形であるので 求める四角形は正方形であるといえる




中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube



長方形の対角線の求め方 白丸くん



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 7819 Pdf



ストークスの回転定理 の証明 その1 微小長方形での証明 Jo3krpの独り言


